Rust Backend

In this part, we explain the Rust code that acts as a backend server and makes the functionalities of the Transparency Dictionary and the zkSNARKs accessible via APIs. The code up to now serves to a large extent still the illustration of the individual function modes and deviates at some places at the theory explained before somewhat. It is further developed in the course of the time around concrete questions to verifiable programs, which do not reveal anything over the used data to solve. The always up to date code can be found here.

First, we go into the implementation of the most important data structure, namely the indexed merkle trees. Then we look at the current implementation of the zkSNARKs, which can still be optimized in various places in future iterations. Finally, we look at the actix server with different endpoints, with which the current frontend interacts as an example and with which other frontends can interact in the future.

Node structs

To implement indexed Merkle trees we first need the relevant data structures. We distinguish between two different types of nodes: intermediate nodes and leaf nodes. We will take a closer look at these relevant structures in the following.

Both the intermediate nodes and the leaf nodes have a hash value represented as a string. In addition, we encode in each node the information whether it is a left sibling as a boolean value. The nodes differ in the other fields.

Intermediate nodes: The intermediate nodes contain only one field for the left and the right child. We use a reference counter (smarter pointer) here among other things because in Rust it is not allowed that a structure is directly or indirectly a part of itself (recursive data structure). The pointer points to another node, either again an intermediate node or a leaf node.

Leaf nodes: In addition to the information about the positioning in the tree (left or right child), the leaf nodes also contain a hash value consisting of the following values:

active: true or false whether the current leaf node is active or inactive
label: a string in which the key of the key-value pair is stored
value: a string where the value of the key-value pair is stored
next: a string where the next larger (hexadecimal) label is stored

Node structs & enum

#[derive(Serialize, Deserialize, Debug, Clone)]
pub struct InnerNode {
    pub hash: String,
    pub is_left_sibling: bool,
    pub left: Rc<Node>,
    pub right: Rc<Node>,
}

#[derive(Serialize, Deserialize, Debug, Clone)]
pub struct LeafNode {
    pub hash: String,
    pub is_left_sibling: bool,
    pub active: bool,
    pub value: String,
    pub label: String,
    pub next: String,
}

#[derive(Serialize, Deserialize, Debug, Clone)]
pub enum Node {
    Inner(InnerNode),
    Leaf(LeafNode),
}

Node functionalities

Now that we have the structures and the node-enum, we can go into more detail about the very simple functions. I will not explain obvious things further, but just mention that the function is there.

We take a look at the functions that provide some sort of getter or setter for the node structures. We need to provide the different getter and setter because while we have overlaps of fields for both the InnerNode and LeafNode types, we cannot access them directly through the node enum. The get_hash function is written out in full, while the other "getter" and "setter" are only implied, but the principle is the same: we have to distinguish within the logic whether we are dealing with the type Node::Inner(...) or with Node::Leaf(...). In get_hash we still access the same field after the distinction, but since in the current implementation InnerNode and LeafNode are different structures and Rust can't tell if fields overlap, this is one way to access the hash value in the code itself. Similar implementations exist for is_left_sibling and is_active. Just note that by definition a Node::Inner is always active, so the is_active method always returns true in the case of an intermediate node.

The setter methods set_left_sibling_value and set_node_active set the respective value as the name suggests, but also with the exception that the active value for Node::Inner() is not set because the field does not exist and is always treated as "active" anyway.

The initialize_leaf() method receives the components of the sha256 hash value of a leaf node together with the information whether it is a left child (the boolean value is_left) as parameters. The convention is set that the values are parsed in the order active, label, value, next into a string which is enclosed with H(). When a leaf is initialized, the sha256 hash value created from it is assigned to the hash field and the leaf is initialized with the remaining values passed as parameters.

The add_left and add_right methods set the left and right children, respectively, and is accordingly implemented only for intermediate nodes, since leaf nodes have no children. Similarly, the update_next_pointer function updates the next pointer of a leaf node, since this field exists only for leaves.

Finally, we look at the generate_hash function, which it can be applied to an instance of the node-enum and calculates the current hash value in each case. As usual, we must first distinguish whether the node is an intermediate node or a leaf node. If it is an intermediate node, the hash is calculated from the two hash values of the child and looks something like this: H({left_child} || {right_child}). In the case of a leaf node, we have already talked above about the convention and the fields required for it. In the Node::Leaf() arm of the match statement, this hash is calculated from the given parameters and the hash value is set to this value.

Now let's look at the indexed Merkle trees, which we want to create using the node data structures based on inner and leaf nodes.

Node functions

impl Node {
    pub const EMPTY_HASH: &'static str = "0000000000000000000000000000000000000000000000000000000000000000";
    pub const TAIL: &'static str = "FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF";

    pub fn get_hash(&self) -> String {
        match self {
            Node::Inner(inner_node) => inner_node.hash.clone(),
            Node::Leaf(leaf) => leaf.hash.clone(),
        }
    }

    pub fn is_left_sibling(&self) -> bool // ...

    pub fn is_active(&self) -> bool // ...

    pub fn set_left_sibling_value(&mut self, is_left: bool) // ...

    pub fn set_node_active(&mut self) // ...

    pub fn initialize_leaf(active: bool, is_left: bool, label: String, value: String, next: String) -> Self {
        let hash = format!("H({}, {}, {}, {})", active, label, value, next);
        let leaf = LeafNode {
            hash: sha256(&hash),
            is_left_sibling: is_left,
            active,
            value,
            label,
            next
        };
        Node::Leaf(leaf)
    }

    pub fn add_left(&mut self, left: Rc<Self>) {
        if let Node::Inner(inner) = self {
            inner.left = left;
        }
    }

    pub fn add_right(&mut self, right: Rc<Self>) // ...

    pub fn update_next_pointer(new_old_node: &mut Self, new_node: &Self) // ...

    pub fn generate_hash(&mut self) {
        match self {
            Node::Inner(inner_node) => {
                let hash = format!("H({} || {})", inner_node.left.get_hash(), inner_node.right.get_hash());
                inner_node.hash = sha256(&hash);
            }
            Node::Leaf(leaf) => {
                let hash = format!("H({}, {}, {}, {})", leaf.active, leaf.label, leaf.value, leaf.next);
                leaf.hash = sha256(&hash);
            }
        }
    }
}

Indexed Merkle Tree

Now that we have the structures and the node-enum, we can go into more detail about the very simple functions. I will not explain obvious things further, but just mention that the function is there.

Struct

The struct of the indexed Merkle tree is discussed relatively quickly in this implementation, because it consists of only one field: a vector of nodes, i.e. inner - and leaf nodes.

In addition to the struct, we define a function that gets a set of nodes (possibly an entire tree in the form of a node vector) and sets the is_left_sibling value for each node using the set_left_sibling_value() function discussed in the previous section. In this way, we save on this code the match-distinction of whether it is an intermediate node or a leaf node.

Implementation

The implementation of the Indexed Merkle tree structure first has two functions that handle the creation of a tree: new() and initialize().
new() is used in conceivable scenarios when a tree is to be created from several nodes that already exist and are thus passed to the function, while initialize() initializes an empty tree with size-many leaf nodes.
By definition, in an empty tree all leaf nodes except the first (index = 0) are inactive and all empty nodes have the empty hash (64 zeros) as both label and value. The next pointer of the empty nodes is set to the "highest" hash value (64 ones). In both functions the calculate_root() function is called, which we will look at later, but as the name already suggests, however, this function performs the recursive (re)calculation of the Merkle root.

Root calculation

Regardless of the (helper) functions create_tree_from_redis and create_inner_node, which do exactly what the names say, let's now take a closer look at the calculate_root function just mentioned, which internally uses the calculate_next_level function.

We perform the (re)calculation based on the existing data, i.e. the leaf nodes. For this reason, the first step is to filter out any (possibly old) intermediate nodes that may currently exist and save the result. All intermediate nodes are then removed from the current structure.
We then start (re)calculating the parent or intermediate nodes, for which we use the calculate_next_level function. In this case, we always iterate over one two pairs of (leaf) nodes at a time and (re)calculate the parent node based on these nodes and the index (to be able to determine if the resulting node is a left or right child in the tree). In this recalculation, as implemented in the calculate_next_level function, the first node of the node pair (i.e., with index 0) is the left child and the second node is the right child. We then add the recalculated node to the entire node list of the Indexed Merkle Tree structure and cache the result (the first-level parent nodes) in a parents vector.
Finally, we iterate over pairs of intermediate nodes in the parents vector until there is only one element left in the parents vector, which then means that we have computed the Merkle root. Since the root would (theoretically) be a left child node, we set this value to false for completeness.

Before we get into the creation of Merkle proofs in the next section, four more functions of the Indexed Merkle Trees should be mentioned here for the sake of completeness:

get_root() - returns the entire root node with all its properties.
get_commitment() - returns the hash value of the current root node
find_node_index(node: Node) - searches for a node passed as parameter and returns the index as option if the search was successful, otherwise None.
find_leaf_by_label(label: &String) - searches through all leaf nodes for a label, returns the node containing the label as option if the search was successful, otherwise None.

Indexed Merkle Tree struct

#[derive(Serialize, Deserialize, Clone)]
pub struct IndexedMerkleTree {
    nodes: Vec<Node>,
}

pub fn update_node_positions(nodes: Vec<Node>) -> Vec<Node> {
    nodes.into_iter()
        .enumerate()
        .map(|(i, mut node)| {
            let is_left_sibling = i % 2 == 0;
            node.set_left_sibling_value(is_left_sibling);
            node
        })
        .collect()
}


impl IndexedMerkleTree {
    pub fn new(nodes: Vec<Node>) -> Self {
        let parsed_nodes = update_node_positions(nodes);
        let tree = Self { nodes: parsed_nodes };
        tree.calculate_root()
    }

    pub fn initialize(size: usize) -> IndexedMerkleTree {
        // ...
        let mut tree = IndexedMerkleTree {
            nodes: Vec::new(),
        };
        for i in 0..size {
            let is_active_leaf = i == 0;
            let is_left_sibling = i % 2 == 0;
            let value = Node::EMPTY_HASH.to_string();
            let label = Node::EMPTY_HASH.to_string();
            let node = Node::initialize_leaf(is_active_leaf, is_left_sibling, value, label, Node::TAIL.to_string());
            tree.nodes.push(node);
        }
        tree.calculate_root()
    }

    pub fn create_tree_from_redis(derived_dict: &mut redis::Connection, input_order: &mut redis::Connection) -> Self  //...

    pub fn create_inner_node(left: Node, right: Node, index: usize) -> Node // ...

    pub fn calculate_next_level(&mut self, current_nodes: Vec<Node>) -> Vec<Node> {
        let mut next_level_nodes: Vec<Node> = Vec::new();

        for (index, node) in current_nodes.chunks(2).enumerate() {
            let new_node = IndexedMerkleTree::create_inner_node(node[0].clone(), node[1].clone(), index);
            next_level_nodes.push(new_node.clone());
            self.nodes.push(new_node);
        }
        next_level_nodes
    }

    fn calculate_root(mut self) -> IndexedMerkleTree {
        let leaves: Vec<Node> = self.nodes.clone().into_iter().filter(|node| matches!(node, Node::Leaf(_))).collect();
        self.nodes = leaves.clone();

        let mut parents: Vec<Node> = self.calculate_next_level(leaves);

        while parents.len() > 1 {
            let processed_parents: Vec<Node> = self.calculate_next_level(parents);
            parents = processed_parents;
        }

        let root = self.nodes.last_mut().unwrap();
        root.set_left_sibling_value(false);
        self
    }

    pub fn get_root(&self) -> &Node // ...

    pub fn get_commitment(&self) -> String // ...

    pub fn find_node_index(&self, node: &Node) -> Option<usize> // ...

    pub fn find_leaf_by_label(&self, label: &String) -> Option<Node> // ...

}

Merkle Proofs

In this section I will explain the current implementation of Merkle Proofs, as well as the Insert- and Update-Proofs that build on them. While more specific details can be found in the chapters, let's just briefly recall the general structure:

A Merkle Proof is a path starting from the leaf node for which we want to create the proof to the root. The proof includes each sibling node on the path from the leaf itself to the root. These sibling nodes are each necessary for computing the "next level node", from which in turn the sibling node is added to the proof path. In this way, one can recalculate the root at any time and compare it with the root transmitted in the proof. Due to the special structure of the leaves in our case, which among other things includes an index which makes the leaves sortable, these Merkle proofs can be used not only to prove that a leaf node is contained (Proof-of-Membership), but also that a leaf node is not contained (Proof-of-Non-Membership).

In Deimos, the Proof-of-Update is a concatenation of two Merkle Proofs. With the first Merkle proof it is shown that the leaf with the old value is contained, with the second Merkle proof it was shown that now at the same place (at the same index) the leaf with the updated value is present.

Based on this, the Proof-of-Insert is a string of five Merkle proofs. The first Merkle proof ensures in the form of a Proof-of-Non-Memberships that the value to be inserted does not yet exist. Then two Proof-of-Updates. First the pointer of the leaf which encloses the new index to be inserted is updated and afterwards a previously inactive leaf with the values of the new leaf. This is shown in each case with two Merkle proofs in the form of a Proof-of-Update.

Analogous to the repetition, we define the relevant types (tuples). The Merkle proof consists of two option values: a string containing the commitment, i.e. the Merkle root, and a vector of nodes containing the path described above. The first element in this vector is always the leaf node for which the Merkle proof is to be performed. As explained above, the Update Proof consists of two Merkle proofs and the Insert Proof consists of one Merkle proof (Proof-Of-Non-Membership) and two Update Proofs.

For the Proof-Of-Membership we pass an index to the generate_proof_of_membership()-function, which must not be confused with the indexing by sortable label values. The index passed as a parameter of the function is the "position" of the leaf in the tree, so if we assume that the first leaf is at the position index 0, this value must simply be incremented by one for each further leaf.

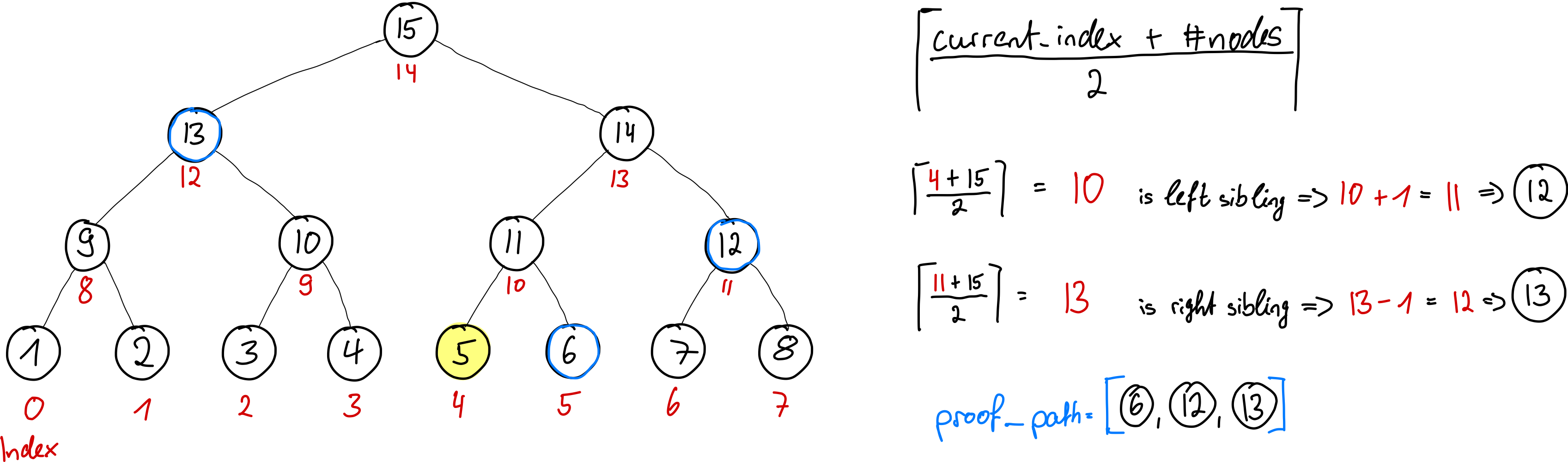
If the passed index is not valid, for example greater than the number of all leaves in the tree, we do not return a proof, but the value None for both option variants. If the index is valid, we create a vector that stores nodes and will contain our proof path. We add the node itself as the first element to the proof path. We also note the current index, which we will change as the proof progresses (depending on the level in the tree). We just run the proof in a loop. We do this as long as the current index we will increment below is smaller than the index of the Merkle root (the last element in the node vector of the Indexed Merkle Tree instance). We first check if the current index is that of a left or right node in the tree. If it is that of a left node, we add one to the current index so that we can get the sibling node or conversely we subtract one for the sibling node of a right node. We then add the node at the calculated position of the sibling node into the array of the proof path and finally calculate the new index. We now need to go up one level in the tree and calculate the position of the sibling node of the parent node of the previously treated nodes. To do this, we convert our current index to a floating point number, add the total number of nodes in the tree, divide the result by two, and then round up. Let's see why in a short example calculation for a total Merkle tree of 8 leaves (15 elements) and a proof-of-membership of the node at index 4:

Merkle Proof Types and Proof-Of-Membership


pub type MerkleProof = (Option<String>, Option<Vec<Node>>);
pub type UpdateProof = (MerkleProof, MerkleProof);
pub type InsertProof = (MerkleProof, UpdateProof, UpdateProof);


impl IndexedMerkleTree {

    pub fn generate_proof_of_membership(&self, index: usize) -> MerkleProof {
        if index >= self.nodes.len() {
            return (None, None);
        }

        let mut proof: Vec<Node> = vec![];
        let mut current_index = index;

        let leaf_node = self.nodes[current_index].clone();
        proof.push(leaf_node);

        while current_index < self.nodes.len() - 1 {
            let sibling_index = if current_index % 2 == 0 { current_index + 1 } else { current_index - 1 };
            let sibling_node = self.nodes[sibling_index].clone();
            proof.push(sibling_node);
            current_index = ((current_index as f64 + self.nodes.len() as f64) / 2.0).ceil() as usize;
        }
        let root = self.get_commitment();

        (Some(root.clone()), Some(proof))
    }

}

Proof-of-Non-Membership

Building on the Proof-of-Membership, we now generate the Proof-of-Non-Membership. We pass the node for which we want to perform the proof to the generate_proof_of_non_membership() function. First we parse this node into a leaf, i have to add a better error handling if this does not work. We then iterate over all leaves of the tree, since we can only perform the proof with the leaves. With the enumerate() function we make sure that we can access the current index as well as the current node during each iteration. We parse the current node into a leaf node and use the BigInt::from_str_radix() function to convert the label value and next pointer of the current node and the label value of the node for which we are performing the Proof-of-Non-Membership to an integer. After the conversion, we check which node's label and next-pointer values enclose the label of the new node. Subsequently, we perform a Proof-of-Membership for this node and also return the index found, since we can use this index in the further process.

Proof-Of-Non-Membership

pub fn generate_proof_of_non_membership(&self, node: &Node) -> (MerkleProof, Option<usize>) {
    let given_node_as_leaf = match node {
        Node::Leaf(leaf) => leaf,
        _ => unreachable!(),
    };

    let leaves: Vec<Node> = self.nodes.clone().into_iter().filter(|node| matches!(node, Node::Leaf(_))).collect();
    let index = leaves.iter().enumerate().find_map(|(index, current_node)| {

        let current_leaf = match current_node {
            Node::Leaf(leaf) => leaf,
            _ => unreachable!(),
        };

        let current_label = BigInt::from_str_radix(&current_leaf.label, 16).unwrap();
        let current_next = BigInt::from_str_radix(&current_leaf.next, 16).unwrap();
        let new_label = BigInt::from_str_radix(&given_node_as_leaf.label, 16).unwrap();

        if current_label < new_label && new_label < current_next {
            Some(index)
        } else {
            None
        }
    });

    if let Some(index) = index {
        (self.generate_proof_of_membership(index), Some(index))
    } else {
        ((None, None), None)
    }
}

Proof-of-Update

The Proof-of-Update is now pretty straight forward. We pass the index of the node that is to be updated and the node whose values are to be stored at the location. To do this, we first use the generate_proof_of_membership() method to prove that the "old" node exists and then update the node at the selected index. After the update, we recalculate the Merkle root and perform the Proof-of-Membership with the updated node. We then return the proof before and the proof after the update, as well as the modified self instance for reuse in other functions.

Proof-of-Update

pub fn generate_proof_of_update(mut self, index:usize, new_node: Node) -> (UpdateProof, Self) {
    let old_proof = self.generate_proof_of_membership(index);

    self.nodes[index] = new_node;
    self = self.clone().calculate_root();

    let new_proof = self.clone().generate_proof_of_membership(index);

    ((old_proof, new_proof), self)
}

Proof-of-Insert

The Proof-of-Insert returns a Proof-of-Non-Membership (Merkle proof) as defined before, as well as two Proof-of-Updates. The function receives the node to be inserted as a parameter and first performs the Proof-of-Non-Membership, whereby we get back not only the proof itself but also the index at which the new node would have to be present if it already existed, and this is accordingly also the location at which the node must be inserted. By knowing only this index, we can edit the node that is currently at this location. We get the node from the nodes vector, update the next pointer, and generate the resulting new hash value. Before we update the node in the tree, we create the first update proof for updating the next pointer. Since we already make the relevant changes in the generate_proof_of_update() method and want to change the value behind the self-reference, we dereference it and set it to the tree changed by the Proof-of-Update. After Proof-of-Update for the next pointer of the existing node, we follow up in the Proof-of-Insert by updating an inactive, empty node with the values of the new node. We iterate over all nodes and pick the next inactive node, remembering the index. The expect() function should not be executed at any time, since the create_tree_from_redis() function considers the case in which the tree capacity must be doubled. However, there is certainly room for code improvement at this point. After we have found the index of the next inactive leaf, we create the second Proof-of-Update with this index and return all created proofs.

Proof-of-Insert

pub fn generate_proof_of_insert(&mut self, new_node: &Node) -> (MerkleProof, UpdateProof, UpdateProof) {
    let (proof_of_non_membership, old_index) = self.clone().generate_proof_of_non_membership(new_node);

    let mut new_old_node = self.nodes[old_index.unwrap()].clone();
    Node::update_next_pointer(&mut new_old_node, new_node);
    new_old_node.generate_hash();
    let (first_update_proof, updated_self) = self.clone().generate_proof_of_update(old_index.unwrap(), new_old_node.clone());

    *self = updated_self;

    let mut new_index = None;
    for (i, node) in tree.nodes.iter_mut().enumerate() {
        if !node.is_active() {
            new_index = Some(i);
            break;
        }
    }
    let new_index = new_index.expect("Unable to find an inactive node.");

    let second_update_proof = tree.generate_proof_of_update(new_index, new_node.clone());

    (proof_of_non_membership, first_update_proof, second_update_proof)
}

Verifying the proofs

The verify_merkle_proof() function takes a Merkle proof and returns a boolean value: true if the proof could be verified and false otherwise. We first verify that the Options of the MerkleProof type actually contain values. Then we take the first node of the path, which corresponds to the node for which we did the proof. Now we iterate over the vector of the remaining nodes starting at the second element and calculate the hash values depending on whether it holds a left or right element. When we have calculated all the hash values, the final hash value must be equal to the root contained in the proof. If this is the case we return true, otherwise false.

To verify a Proof-of-Update we have to perform the verify_merkle_proof() function for both Merkle proofs and for the Proof-of-Insert we can then reuse the verify_update_proof() function analogous to the above to verify both the Proof-of-Non-Membership and the two Proof-of-Updates.

Proof-of-Insert

fn verify_merkle_proof(proof: &MerkleProof) -> bool {
    match proof {
        (Some(root), Some(path)) => {
            let mut current_hash = path[0].get_hash();
    
            for node in path.iter().skip(1) {
                let hash = if node.is_left_sibling() {
                    format!("H({} || {})", node.get_hash(), current_hash)
                } else {
                    format!("H({} || {})", current_hash, node.get_hash())
                };
                current_hash = sha256(&hash);
            }
            return &current_hash == root;
        },
        _ => false
    }
}

pub fn verify_update_proof((old_proof, new_proof): &UpdateProof) -> bool {
    IndexedMerkleTree::verify_merkle_proof(old_proof) && IndexedMerkleTree::verify_merkle_proof(new_proof)
}

pub fn verify_insert_proof(non_membership_proof: &MerkleProof, first_proof: &UpdateProof, second_proof: &UpdateProof) -> bool {
    IndexedMerkleTree::verify_merkle_proof(non_membership_proof) && IndexedMerkleTree::verify_update_proof(first_proof) && IndexedMerkleTree::verify_update_proof(second_proof)
}

zkSNARK circuits

The second module creates the arithmetic circuits for the zkSNARKs. The theory surrounding the R1CS and the idea of the SIMD R1CS, which has not yet been implemented in code, will be described in more detail here, so we will focus exclusively on the current implementation below. As noted, the zkSNARKs are used to primarily verify a whole set of Merkle proofs in one step. The goal here is that the public parameters simply represent the current and previous epochs, and we can use the zkSNARKs to prove the correct interactions between the two epochs.

First we look at the two functions hext_to_scalar() and recalculate_hash_as_scalar(). hext_to_scalar() receives a string and makes a scalar value out of it from the module of the elliptic curve BLS12. To do this, we first parse the hex_string into a byte array and fill the initial 32-bytes with zeros in front. This does not change the value of the hash, but we can then use the Scalar::from_bytes_wide() function instead of the Scalar::from_bytes() function. I won't go deeper into the explanation at this point (yet), as first the big picture should be clearer, but this is related to the fact that with the use of the from_bytes() method, an error occurs if the hash value passed is greater than the group order at BLS12. The from_bytes_wide() method, on the other hand, reduces the given hex value modulo the 381-bit prime and thus does not raise an error if the hash value is 256 bits larger than the group order (255 bits). Furthermore, the recalculate_hash_as_scalar() function is defined, which recalculates a given path of nodes (proof path in Merkle proof) and returns the result as a scalar.

Based on these functions, we now look at the generation of the Proof-of-Update and Proof-of-Insert circuits.

In the following, we will repeatedly define variables in a so-called constraint system. This is our possibility to create R1CS with the help of bellman. We will create linear combinations within the constraint system and can define (allocate) the variables with two different methods: alloc() and alloc_input(). The difference lies in the accessibility of the variables to the verifier. alloc() defines a private variable in the circuit, i.e. a variable that will not be visible to the verifier, while alloc_input() represents a so-called public parameter within the linear combinations. In addition to the ConstraintSystem, the function to create the circuit for a Proof-of-Update receives the old and new roots as well as the associated Merkle proofs (Merkle paths). We first allocate the two roots as private variables in the circuit, since the individual intermediate results within an epoch should not necessarily be public and thus details are kept secret. We then use the recalculate_hash_as_scalar() function to calculate the root based on the path and allocate the recalculated result in the circuit as well. With the enforce() method we enforce that the correctness of the following linear combination is given:

\text{Let } z_1 = \text{old\_root}, \\\text{let }z_2 = \text{new\_root},\\ v^T=(one,x,out,y)\\ v^T \cdot(0,1,0,0) * v^T \cdot(1,0,0,0) = v^T \cdot(0,0,0,1)\\ \equiv x * 1 = y

which means that the Merkle root passed is equal to the Merkle root computable by the path.

The function to generate the Proof-of-Non-Membership circuit is now analogous and easy to understand. A difference between the two functions is that if the Proof-of-Non-Membership function has no error within the linear combinations and simply passes through it returns no value, the Proof-of-Update function on the other hand returns the last computed root. So we can reuse this in the following and use the output of an update as input of the next proof to create more efficient circuits.

At this point a word about the structure of the enforce method: the method has four parameters. As said, the function is used to add a condition in the form of an R1CS equation ( $A*B=C$ ) to the constraint system. The first parameter assigns a unique name to the particular equation. The other three parameters are anonymous functions that define each linear combination ( $A,B,C$ ). Each of the parameters receives the current linear combination as a parameter of an anonymous function and uses the + operator to add the passed variable to this linear combination. At this point, the + operation is therefore not to be understood as a classical addition, but describes the addition of the variable to the currently existing equation of the linear combination.

zkSNARKs

pub fn hex_to_scalar(hex_string: &str) -> Scalar {
    let byte_array: [u8; 32]  = hex::decode(hex_string).unwrap().try_into().unwrap();
    let mut wide = [0u8; 64];
    wide[..32].copy_from_slice(&byte_array); 
    Scalar::from_bytes_wide(&wide)
}

pub fn recalculate_hash_as_scalar(path: &[Node]) -> Scalar {
    let mut current_hash = path[0].get_hash();
    for i in 1..(path.len()) {
        let sibling = &path[i];
        if sibling.is_left_sibling() {
            current_hash = sha256(&format!("H({} || {})", &sibling.get_hash(), current_hash));
        } else {
            current_hash = sha256(&format!("H({} || {})", current_hash, &sibling.get_hash()));
        }
    }
    hex_to_scalar(&current_hash.as_str())
}

fn proof_of_update<CS: ConstraintSystem<Scalar>>(
    cs: &mut CS,
    old_root: Scalar,
    old_path: &[Node],
    new_root: Scalar,
    new_path: &[Node],
) -> Result<Scalar, SynthesisError> {
    let root_with_old_pointer = cs.alloc(|| "first update root with old pointer", || Ok(old_root))?;
    let root_with_new_pointer = cs.alloc(|| "first update root with new pointer", || Ok(new_root))?;

    let recalculated_root_with_old_pointer = recalculate_hash_as_scalar(&old_path);
    let recalculated_root_with_new_pointer = recalculate_hash_as_scalar(&new_path);

    let allocated_recalculated_root_with_old_pointer = cs.alloc(|| "recalculated first update proof old root", || Ok(recalculated_root_with_old_pointer))?;
    let allocated_recalculated_root_with_new_pointer = cs.alloc(|| "recalculated first update proof new root", || Ok(recalculated_root_with_new_pointer))?;

    cs.enforce(|| "first update old root equality", |lc| lc + allocated_recalculated_root_with_old_pointer, |lc| lc + CS::one(), |lc| lc + root_with_old_pointer);
    cs.enforce(|| "first update new root equality", |lc| lc + allocated_recalculated_root_with_new_pointer, |lc| lc + CS::one(), |lc| lc + root_with_new_pointer);

    Ok(recalculated_root_with_new_pointer)
}

fn proof_of_non_membership<CS: ConstraintSystem<Scalar>>(
    cs: &mut CS,
    non_membership_root: Scalar,
    non_membership_path: &[Node],
) -> Result<(), SynthesisError> {
    let allocated_root = cs.alloc(|| "non_membership_root", || Ok(non_membership_root))?;
    let recalculated_root = recalculate_hash_as_scalar(non_membership_path);
    let allocated_recalculated_root = cs.alloc(|| "recalculated non-membership root", || Ok(recalculated_root))?;

    cs.enforce(
        || "non-membership root check",
        |lc| lc + allocated_root,
        |lc| lc + CS::one(),
        |lc| lc + allocated_recalculated_root,
    );

    Ok(())
}

After defining and explaining the helper functions, we now look at the rest of the circuit creation. For this we define first for the update and insert case a struct and combine these afterwards to a batch of different update and insert proofs, since these occur within an epoch mixed and we want to create the zkSNARK for all proofs of an epoch. The UpdateMerkleProofCircuit consists of the same parts as a "normal" Proof-of-Update, but with adjusted values (in this case the root is already required as a scalar value). The InsertMerkleProofCircuit is also easy to understand with the existing definitions: a Proof-of-Non-Membership followed by two Proof-of-Update circuits. We combine these structures into an enum ProofVariantCircuit and build on top of it the BatchMerkleProofCircuit structure, which takes two commitments and a vector of arbitrary circuits to the proof types defined earlier. The commitments here are the old commitment (from the previous epoch compared to the requested epoch) and the commitment of the current (requested) epoch.

For each of the circuits defined above, we need to implement a so-called circuit-trait in bellman, which always contains a synthesize() function that creates the circuit. We can simply use the already created helper functions at these points, and so the synthesize function of the update circuit contains only the already considered proof_of_update() function, and the synthesize() function of the insert circuit contains both the proof_of_non_memberhsip() function, and two proof_of_update functions. The "old" input of the second proof_of_update function depends on the calculation of the first proof_of_update function, because we want to ensure that the results are not considered independently but consecutively.

Circuits

#[derive(Clone)]
pub struct UpdateMerkleProofCircuit {
    pub old_root: Scalar,
    pub old_path: Vec<Node>,
    pub updated_root: Scalar,
    pub updated_path: Vec<Node>,
}

#[derive(Clone)]
pub struct InsertMerkleProofCircuit {
    pub non_membership_root: Scalar,
    pub non_membership_path: Vec<Node>,
    pub first_merkle_proof: UpdateMerkleProofCircuit,
    pub second_merkle_proof: UpdateMerkleProofCircuit,
}


#[derive(Clone)]
pub enum ProofVariantCircuit {
    Update(UpdateMerkleProofCircuit),
    Insert(InsertMerkleProofCircuit),
}

#[derive(Clone)]
pub struct BatchMerkleProofCircuit {
    pub old_commitment: Scalar,
    pub new_commitment: Scalar,
    pub proofs: Vec<ProofVariantCircuit>,
}

impl Circuit<Scalar> for InsertMerkleProofCircuit {
    fn synthesize<CS: ConstraintSystem<Scalar>>(self, cs: &mut CS) -> Result<(), SynthesisError> {
        match proof_of_non_membership(cs, self.non_membership_root, &self.non_membership_path) {
            Ok(_) => (),
            Err(_) => return Err(SynthesisError::AssignmentMissing),
        }

        let first_proof = proof_of_update(cs, self.first_merkle_proof.old_root, &self.first_merkle_proof.old_path, self.first_merkle_proof.updated_root, &self.first_merkle_proof.updated_path);
        let second_update = proof_of_update(cs, first_proof.unwrap(), &self.second_merkle_proof.old_path, self.second_merkle_proof.updated_root, &self.second_merkle_proof.updated_path);

        match second_update {
            Ok(_) => Ok(()),
            Err(_) => return Err(SynthesisError::Unsatisfiable),
        }
    }
}

impl Circuit<Scalar> for UpdateMerkleProofCircuit {
    fn synthesize<CS: ConstraintSystem<Scalar>>(self, cs: &mut CS) -> Result<(), SynthesisError> {
        match proof_of_update(cs, self.old_root, &self.old_path, self.updated_root, &self.updated_path) {
            Ok(_) => Ok(()),
            Err(_) => return Err(SynthesisError::Unsatisfiable),
        }
    }
}

Now all "preparatory work" is done to be able to implement the circuit of the BatchMerkleProofCircuit structure or the synthesize() function defined with it.

The implementation of the synthesize()-function is built up from the basic principles exactly like the synthesize()-functions of the previous circuit creation. Inside the function, we first look at how the old root must look like according to the proofs and whether it matches the passed commitment.

To do this, we first distinguish of what type the first proof is. If it is an Proof-of-Update the old commitment is the old root contained in the first UpdateProof, in case of an Proof-of-Insert it is the root of the non-membership proof. In the following, we create two variables in the constraint system: provided_old_commitment is the commitment that will be passed to the BatchedMerkleProof. This is to be one of the public inputs of the zkSNARK, accordingly we use the alloc_input() method as described before, since this defines variables for public parameters. The root that must match the old commitment is the one we extracted from the Merkel proof and will not be a public input, accordingly we allocate the "private" variable using the alloc() function. Then, based on the proof vector, we recalculate the current commitment, which is also the root after the last option within the epoch.

To do this, we iterate over all existing proofs and again distinguish between the type of each proof. In the case of a Proof-of-Update, the currently computed commitment is set to the returned value of the update proof (see above). In the case of an Proof-of-Insert, we first let check whether the requirements within the proof_of_non_membership() function are met, so it can be executed accordingly. Then we calculate the first update operation and use the calculated result as input for the second update proof. In this case, we set the variables for storing the recalculated commitment "new_commitment" to the output of the second update proof.

Using the enforce() method, we force the recalculated commitment and the passed commitment to match. The latter is provided as public input as well and the recalculation is provided as a private input parameter. So only on the basis of the two passed commitments as public parameters the recalculation is verified on the basis of proofs that took place within this epoch.

BatchMerkleProofCircuit

impl Circuit<Scalar> for BatchMerkleProofCircuit {
    fn synthesize<CS: ConstraintSystem<Scalar>>(self, cs: &mut CS) -> Result<(), SynthesisError> {
        let old_root = match &self.proofs[0] {
            ProofVariantCircuit::Update(update_proof_circuit) => update_proof_circuit.old_root,
            ProofVariantCircuit::Insert(insert_proof_circuit) => insert_proof_circuit.non_membership_root,
        };

        let provided_old_commitment = cs.alloc_input(|| "provided old commitment", || Ok(self.old_commitment))?;
        let old_commitment_from_proofs = cs.alloc(||"old commitment from proofs", || Ok(old_root))?;

        cs.enforce(
            || "old commitment check",
            |lc| lc + provided_old_commitment,
            |lc| lc + CS::one(),
            |lc| lc + old_commitment_from_proofs,
        );

        let mut new_commitment: Option<Scalar> = None;
        for proof_variant in self.proofs {
            match proof_variant {
                ProofVariantCircuit::Update(update_proof_circuit) => {
                    new_commitment = Some(proof_of_update(
                        cs,
                        update_proof_circuit.old_root,
                        &update_proof_circuit.old_path,
                        update_proof_circuit.updated_root,
                        &update_proof_circuit.updated_path,
                    )?);
                }
                ProofVariantCircuit::Insert(insert_proof_circuit) => {
                    match proof_of_non_membership(cs, insert_proof_circuit.non_membership_root, &insert_proof_circuit.non_membership_path) {
                        Ok(_) => (),
                        Err(_) => return Err(SynthesisError::AssignmentMissing),
                    }

                    let calculated_root_from_first_proof = proof_of_update(cs, insert_proof_circuit.first_merkle_proof.old_root, &insert_proof_circuit.first_merkle_proof.old_path, insert_proof_circuit.first_merkle_proof.updated_root, &insert_proof_circuit.first_merkle_proof.updated_path).expect("first proof of update in insert proof failed");
                    new_commitment =  Some(proof_of_update(cs, calculated_root_from_first_proof, &insert_proof_circuit.second_merkle_proof.old_path, insert_proof_circuit.second_merkle_proof.updated_root, &insert_proof_circuit.second_merkle_proof.updated_path).expect("second proof of update in insert proof failed"));
                }
            }
        }

        let provided_new_commitment = cs.alloc_input(|| "provided commitment", || Ok(self.new_commitment))?;
        let recalculated_new_commitment = cs.alloc(||"recalculated commitment", || Ok(new_commitment.unwrap()))?;

        cs.enforce(
            || "new commitment check",
            |lc| lc + provided_new_commitment,
            |lc| lc + CS::one(),
            |lc| lc + recalculated_new_commitment,
        );

        Ok(())
    }
}

Beside the functions for the creation of the circuits there is another implementation for the BatchMerkleProofCircuit structure, which contain helper functions for the conversion of the Merkle tree structures into the relevant data formats for the proof creation. Thereby there is first the create() function, whose functions are to be sketched here briefly. The function takes as parameters both the old and the new commitment and a vector of different proofs. Within the function the types of the commitments are parsed from strings to scalar values and then the array of proofs is iterated over to perform the same procedure for each proof: to parse the types of the respective commitments into scalar values. At this point we will not take a closer look at the other two functions, since the structure of the individual proofs and their types should be clear and the procedure is identical to the procedure within the create() function.

BatchMerkleProofCircuit helper functions

impl BatchMerkleProofCircuit {
    pub fn create(old_commitment: &String, new_commitment: &String, proofs: Vec<ProofVariant>) -> Result<BatchMerkleProofCircuit, &'static str> {
        let parsed_old_commitment = hex_to_scalar(&old_commitment.as_str());
        let parsed_new_commitment = hex_to_scalar(&new_commitment.as_str());
        let mut proof_circuit_array: Vec<ProofVariantCircuit> = vec![];
        for proof in proofs {
            match proof {
                ProofVariant::Update(update_proof) => {
                    proof_circuit_array.push(BatchMerkleProofCircuit::create_from_update(&update_proof).unwrap());
                },
                ProofVariant::Insert(merkle_proof, first_update, second_update) => {
                    proof_circuit_array.push(BatchMerkleProofCircuit::create_from_insert(&(merkle_proof, first_update, second_update)).unwrap());
                }
            }
        }
        Ok(BatchMerkleProofCircuit {
            old_commitment: parsed_old_commitment,
            new_commitment: parsed_new_commitment,
            proofs: proof_circuit_array,
        })
    }

    pub fn create_from_update(((old_root, old_path), (updated_root, updated_path)): &UpdateProof) -> Result<ProofVariantCircuit, &'static str> { }

    pub fn create_from_insert(proofs: &(MerkleProof, UpdateProof, UpdateProof)) -> Result<ProofVariantCircuit, &'static str> { }
}

Actix server

After all the relevant basics are taken care of, we can move on to enabling interaction with the two Rust modules. For this, we set up a Rust-Actix server that enables endpoints for interaction with the different parts.

I will not go into the technical details of setting up the HTTPS server. The exact code can be seen here, and more information about actix can be found here, among other places. So we'll just get a rough overview and then go into a bit more detail about the asynchrone function intialize_epoch_state, since it plays an important role in initializing the bases. But as said before, a few short notes on the individual parts:

Name
dotenv().ok();
Type
load the dotenv environment file
Description
We load the dotenv file and ignore the errors for now with .ok(). Later we set default values with unwrap_or() in case of error.
Name
KEY_PATH / CERT_PATH
Type
env variables
Description
To set up the HTTPS server we need a certificate. We try to load the environment variables defined in the .env.example comment above as an example. If this fails, we set a dummy variable for the moment
Name
HttpServer::new
Type
cors-settings and services
Description
Within the Lambda function, a CORS (Cross-Origin Resource Sharing) configuration is created, which is applied to the app later in the code. Then, the various APIs associated with a particular function are registered. The server is then bound to IP address 127.0.0.1 and port 8080 and started asynchronously. \text{Commitment}_{t-1}

Creating a basic HTTPS-Server

#[actix_web::main]
async fn main() -> std::io::Result<()> {
  dotenv().ok();

  spawn(async {
      loop {
          intialize_epoch_state().await;
      }
  });

  let key_path = env::var("KEY_PATH").unwrap_or("key.pem".to_string());
  let cert_path = env::var("CERT_PATH").unwrap_or("cert.pem".to_string());

  // ... tls, certificate, priv key settings

  HttpServer::new(|| {
      let cors = Cors::default()
          // .. cors settings
      App::new()
          .wrap(cors)
          .service(update)
          // ...
  })
  .bind_openssl(("127.0.0.1", 8080), builder)?
  .run()
  .await

}

In the following, we first refer to the construction and creation of the server using Actix Web, a powerful web framework for Rust. We will highlight the different APIs and explain the basic procedure of how the ideas and data structures explained theoretically before can be used.